Coordinate Frames and Planes¶
In order to configure and use the lsst.cbp.CoordinateConverter object effectively it is important to understand the following coordinate frames.
If you are a using the CBP to calibrate the telescope then you probably only care about two planes: the pupil plane and the focal plane. However, if you are configuring the CBP then it helps to have some grasp of all of the coordinate frames and planes described here.
But first, a few bits of terminology:
- A coordinate frame is always 3 dimensional. A plane is, of course, 2 dimensional. The only place where confusion is likely is when discussing the pupil, as there is both a pupil frame and a pupil plane.
- The “center” of the telescope or CBP is that point where the azimuth and altitude axes intersect.
Base Frame¶
The base frame is a 3-dimensional coordinate frame that is fixed with respect to the observatory. It is used to express the position of the CBP with respect to the telescope.
The z axis of the base frame must point up. You are free to choose a convenient orientation for the x and y axes, so long as the coordinate system is right handed. It is common to align x and y axes with cardinal points, e.g. x points south and y points east. Your choice primarily affects the configured azimuth and altitude offset.
The origin of the base frame is at the center of the telescope.
Pupil Frame¶
The pupil frame is a frame that is fixed with respect to the primary mirror, and whose x axis points along the optical axis. The origin of the pupil frame is the center of the telescope, just like the base frame.
The pupil frame is a rotation of the base frame, as follows:
- first rotate about the z axis by internal azimuth (see below)
- then rotate about the rotated y axis by internal altitude (see below)
Thus:
- At internal azimuth and altitude = 0 the pupil frame matches the base frame
- At internal azimuth = 90° and altitude = 0 pupil x = base y, pupil y = -base x and pupil z = base z
- At internal azimuth = 0 and altitude = 90° pupil x = base z, pupil z = - base x and pupil y = base y.
Note: there are actually two pupil frames: one for the telescope and one for the CBP. The origin of the CBP pupil frame is at the center of the CBP, as you might expect.
Note: for the telescope, the origin of the pupil plane is typically offset along the optical axis from the origin of the pupil frame; see pupil plane for details.
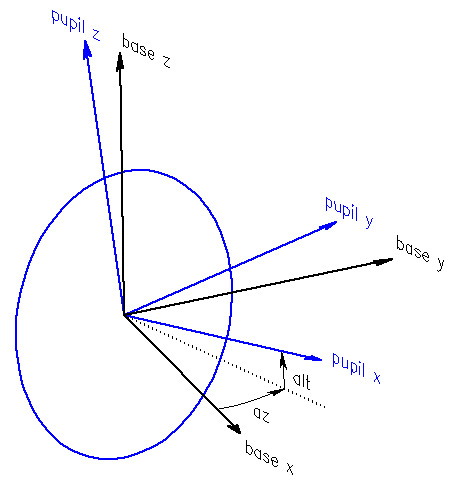
Diagram showing the pupil and base frames. Note that azimuth and altitude are internal angles
Internal Azimuth, Altitude and Rotator¶
Internal azimuth and altitude specify the pointing of the telescope or CBP. Please see pupil frame for details.
Internal rotation angle of the telescope’s camera rotator is defined as the orientation of the focal plane x,y axes relative to the pupil y,z axes. Thus:
- At rotator angle zero the direction of increasing focal plane y is along increasing azimuth and
±xis along the direction of increasing altitude. - At rotator angle 90° the direction of increasing focal plane y is along the direction of decreasing altitude and
±xis along the direction of increasing azimuth.
These angles are called internal because they are used internally by this software. There is no standard convention for azimuth or camera rotator zero point and direction, so in order to support different telescopes, this software also supports observed azimuth, altitude and rotator.
Observed Azimuth, Altitude and Rotator¶
Azimuth, altitude and rotator angle of the telescope or CBP axes, using the conventions of the telescope, but in an ideal frame in which imperfections such as tilt and non-perpendicularity of the axes are ignored. The transformation from “observed” az/alt to commands sent to the axis actuators consists of applying a pointing model, and is left to other software.
In order to accommodate different azimuth and rotator conventions, while simplifying the math, all internal computations are performed using internal angles.
Internal angles are mapped to observed angles using an offset and scale for each axis,
which is specified in lsst.cbp.CoordinateConverterConfig.
Focal Plane¶
The focal plane is a 2-dimensional plane approximation to the actual focal surface, which typically has some curvature. The internal rotation angle is the angle of the focal plane x,y axes with respect to the pupil plane x,y axes.
If the focal plane is rotated such that focal plane y is along pupil frame z, then either focal plane +x or -x will be along pupil frame y. If -x then the x axis of the focal plane and all other 2-dimensional plane positions (pupil plane, focal plane field angle and pupil field angle) are said to be “flipped”. Determining this parity for the telescope and CBP is part of configuration.
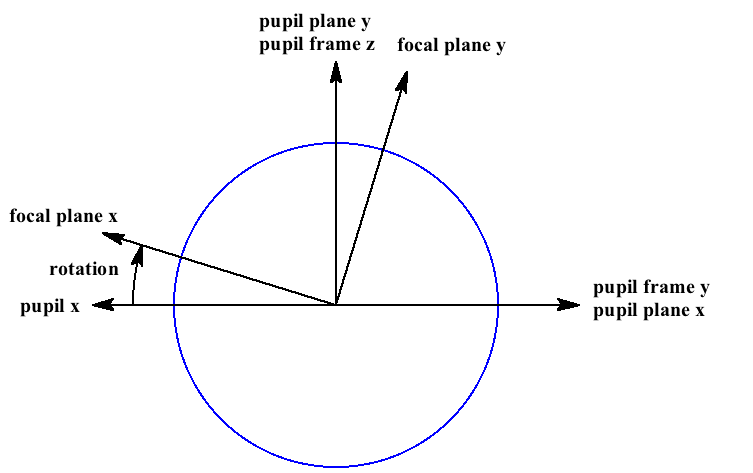
Diagram showing the pupil with the x axis flipped; the pupil frame z axis is pointing straight at you. Rotation is an internal angle
Note that focal plane is the same coordinate system as lsst.afw.cameraGeom.FOCAL_PLANE.
Pupil Plane¶
A 2-dimensional plane approximation to the primary mirror of the telescope. This is used to specify the position of a beam on the telescope pupil.
The pupil plane is the y,z plane of the pupil frame:
- pupil plane ±x is along pupil frame y
- pupil plane y is along pupil frame z
For the telescope, the pupil plane may be configured to be anywhere along the optical axis using configuration parameter telPupilOffset, but the usual location is the front of the primary mirror.
Internally, math is performed using a “centered pupil plane” whose origin is at the center of the telescope.
The CBP has been designed with the optical pupil at the center of the CBP (where the azimuth and altitude axes intersect), and this software relies on that fact.
If the focal plane x axis is flipped then the x axis of all other 2-dimensional plane coordinates are flipped, including this one.
Pupil Field Angle¶
The angle of incidence of a ray on the pupil, expressed in x,y radians. The two components of the field angle define a great circle arc:
- arc length = hypot(x, y)
- bearing = atan2(y, x) with 0 along pupil plane x and 90° along pupil plane y
The incident ray is the pupil x axis offset by this great circle arc.
Focal Plane Field Angle¶
Pupil field angle with the components expressed in focal plane x,y instead of pupil plane x,y. Thus this is a rotation of pupil field angle.
Note that focal plane field angle is the same coordinate system as lsst.afw.cameraGeom.FIELD_ANGLE.
Camera geometry includes a transform from lsst.afw.cameraGeom.FOCAL_PLANE to lsst.afw.cameraGeom.FIELD_ANGLE (
focal plane to focal plane field angle), which models optical distortion.